Mysql索引底层结构和算法

索引的定义

索引是帮助MySQL高效获取数据的排好序的数据结构

索引的数据结构

二叉树

以二叉树为示例的索引工作示例图

image

  • 二叉树如果不平衡, 极端情况下查询效率等同于链表
  • 数据库不使用二叉树作为索引数据结构, 因为数据量过大时,磁盘io次数过多

红黑树

image

工作原理与二叉树一致

  • 数据库不使用红黑树作为索引数据结构, 因为数据量过大时,磁盘io次数过多

Hash表

哈希表也为散列表，由直接寻址改进而来。在哈希的方式下，一个元素k处于h(k)中，即利用哈希函数h，根据关键字k计算出槽的位置。函数h将关键字域映射到哈希表T[0…m-1]的槽位上。

image

上图中哈希函数h有可能将两个不同的关键字映射到相同的位置，这叫做碰撞，在数据库中一般采用链接法来解决。在链接法中，将散列到同一槽位的元素放在一个链表中，如下图所示：

image

InnoDB中采用除法散列函数，冲突机制采用链接法。

Hash索引结构的特殊性，其检索效率非常高，索引的检索可以一次定位，不像B-Tree索引需要从根节点到枝节点，最后才能访问到页节点这样多次的IO访问，所以Hash索引的查询效率要远高于B-Tree索引, 但是Hash索引本身由于其特殊性也带来了很多限制和弊端, 主要有以下这些：

  1. Hash索引仅仅能满足”=”,”IN”和”<=>”查询，不能使用范围查询。哈希索引只支持等值比较查询，包括＝、 IN 、<=> (注意<>和＜＝＞是不同的操作）。 也不支持任何范围查询，例如WHERE price > 100。　　
    由于Hash索引比较的是进行Hash运算之后的Hash值，所以它只能用于等值的过滤，不能用于基于范围的过滤，因为经过相应的Hash算法处理之后的Hash值的大小关系，并不能保证和Hash运算前完全一样。
  2. Hash索引无法被用来避免数据的排序操作。　　
    由于Hash索引中存放的是经过Hash计算之后的Hash值，而且Hash值的大小关系并不一定和Hash运算前的键值完全一样，所以数据库无法利用索引的数据来避免任何排序运算;
  3. Hash索引不能利用部分索引键查询。　　
    对于组合索引，Hash索引在计算Hash值的时候是组合索引键合并后再一起计算Hash值，而不是单独计算Hash值，所以通过组合索引的前面一个或几个索引键进行查询的时候，Hash索引也无法被利用。
  4. Hash索引在任何时候都不能避免表扫描。　　
    前面已经知道，Hash索引是将索引键通过Hash运算之后，将 Hash运算结果的Hash值和所对应的行指针信息存放于一个Hash表中，由于不同索引键存在相同Hash值，所以即使取满足某个Hash键值的数据的记录条数，也无法从Hash索引中直接完成查询，还是要通过访问表中的实际数据进行相应的比较，并得到相应的结果。
  5. Hash索引遇到大量Hash值相等的情况后性能并不一定就会比BTree索引高。　
    对于选择性比较低的索引键，如果创建Hash索引，那么将会存在大量记录指针信息存于同一个Hash值相关联。这样要定位某一条记录时就会非常麻烦，会浪费多次表数据的访问，而造成整体性能低下。

B-Tree(平衡多路查找树)

B-Tree是为磁盘等外存储设备设计的一种平衡查找树。因此在讲B-Tree之前先了解下磁盘的相关知识。

系统从磁盘读取数据到内存时是以磁盘块（block）为基本单位的，位于同一个磁盘块中的数据会被一次性读取出来，而不是需要什么取什么。

InnoDB存储引擎中有页（Page）的概念，页是其磁盘管理的最小单位。InnoDB存储引擎中默认每个页的大小为16KB，可通过参数innodb_page_size将页的大小设置为4K、8K、16K，在MySQL中可通过如下命令查看页的大小：

1
mysql> show variables like 'innodb_page_size';

而系统一个磁盘块的存储空间往往没有这么大，因此InnoDB每次申请磁盘空间时都会是若干地址连续磁盘块来达到页的大小16KB。InnoDB在把磁盘数据读入到磁盘时会以页为基本单位，在查询数据时如果一个页中的每条数据都能有助于定位数据记录的位置，这将会减少磁盘I/O次数，提高查询效率。

B-Tree结构的数据可以让系统高效的找到数据所在的磁盘块。为了描述B-Tree，首先定义一条记录为一个二元组[key, data] ，key为记录的键值，对应表中的主键值，data为一行记录中除主键外的数据。对于不同的记录，key值互不相同。

一棵m阶的B-Tree有如下特性：

  1. 每个节点最多有m个孩子。
  2. 除了根节点和叶子节点外，其它每个节点至少有Ceil(m/2)个孩子。
  3. 若根节点不是叶子节点，则至少有2个孩子
  4. 所有叶子节点都在同一层，且不包含其它关键字信息
  5. 每个非终端节点包含n个关键字信息（P0,P1,…Pn, k1,…kn）
  6. 关键字的个数n满足：ceil(m/2)-1 <= n <= m-1
  7. ki(i=1,…n)为关键字，且关键字从左到右升序排序。
  8. Pi(i=1,…n)为指向子树根节点的指针。P(i-1)指向的子树的所有节点关键字均小于ki，但都大于k(i-1)

B-Tree中的每个节点根据实际情况可以包含大量的关键字信息和分支，如下图所示为一个3阶的B-Tree：

image

每个节点占用一个盘块的磁盘空间，一个节点上有两个升序排序的关键字和三个指向子树根节点的指针，指针存储的是子节点所在磁盘块的地址。两个关键词划分成的三个范围域对应三个指针指向的子树的数据的范围域。以根节点为例，关键字为17和35，P1指针指向的子树的数据范围为小于17，P2指针指向的子树的数据范围为17~35，P3指针指向的子树的数据范围为大于35。

模拟查找关键字29的过程：

  1. 根据根节点找到磁盘块1，读入内存。【磁盘I/O操作第1次】
  2. 比较关键字29在区间（17,35），找到磁盘块1的指针P2。
  3. 根据P2指针找到磁盘块3，读入内存。【磁盘I/O操作第2次】
  4. 比较关键字29在区间（26,30），找到磁盘块3的指针P2。
  5. 根据P2指针找到磁盘块8，读入内存。【磁盘I/O操作第3次】
  6. 在磁盘块8中的关键字列表中找到关键字29。

分析上面过程，发现需要3次磁盘I/O操作，和3次内存查找操作。由于内存中的关键字是一个有序表结构，可以利用二分法查找提高效率。而3次磁盘I/O操作是影响整个B-Tree查找效率的决定因素。B-Tree相对于AVLTree缩减了节点个数，使每次磁盘I/O取到内存的数据都发挥了作用，从而提高了查询效率。

B+Tree

B+Tree是在B-Tree基础上的一种优化，使其更适合实现外存储索引结构，InnoDB存储引擎就是用B+Tree实现其索引结构。

从上一节中的B-Tree结构图中可以看到每个节点中不仅包含数据的key值，还有data值。而每一个页的存储空间是有限的，如果data数据较大时将会导致每个节点（即一个页）能存储的key的数量很小，当存储的数据量很大时同样会导致B-Tree的深度较大，增大查询时的磁盘I/O次数，进而影响查询效率。在B+Tree中，所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上，而非叶子节点上只存储key值信息，这样可以大大加大每个节点存储的key值数量，降低B+Tree的高度。

B+Tree相对于B-Tree有几点不同：

  1. 非叶子节点只存储键值信息。
  2. 所有叶子节点之间都有一个双向链指针。
  3. 数据记录都存放在叶子节点中。

将上一节中的B-Tree优化，由于B+Tree的非叶子节点只存储键值信息，假设每个磁盘块能存储4个键值及指针信息，则变成B+Tree后其结构如下图所示：

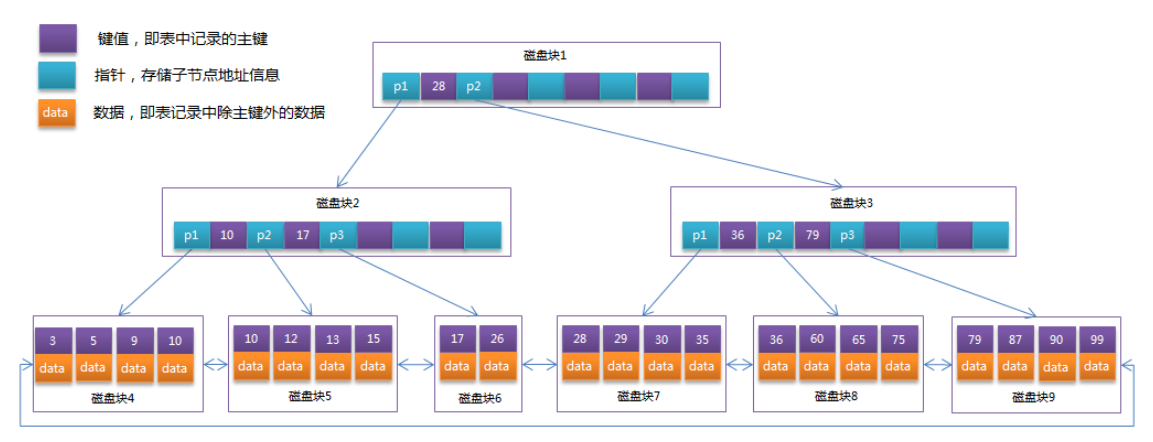
image

通常在B+Tree上有两个头指针，一个指向根节点，另一个指向关键字最小的叶子节点，而且所有叶子节点（即数据节点）之间是一种链式环结构。因此可以对B+Tree进行两种查找运算：一种是对于主键的范围查找和分页查找，另一种是从根节点开始，进行随机查找。

可能上面例子中只有22条数据记录，看不出B+Tree的优点，下面做一个推算：

InnoDB存储引擎中页的大小为16KB，一般表的主键类型为INT（占用4个字节）或BIGINT（占用8个字节），指针类占6个字节，也就是说一个页（B+Tree中的一个节点）中大概存储16KB/(8Byte+6Byte)=1170个键值, 假设一行数据占1kb, 那么3层的b+tree能存储的数据为1170 * 1170 * 16 = 21902400个

实际情况中每个节点可能不能填充满，因此在数据库中，B+Tree的高度一般都在2~4层。mysql的InnoDB存储引擎在设计时是将根节点常驻内存的，也就是说查找某一键值的行记录时最多只需要1到3次磁盘I/O操作。

数据库中的B+Tree索引可以分为聚集索引（clustered index）和辅助索引（secondary index）。上面的B+Tree示例图在数据库中的实现即为聚集索引，聚集索引的B+Tree中的叶子节点存放的是整张表的行记录数据。辅助索引与聚集索引的区别在于辅助索引的叶子节点并不包含行记录的全部数据，而是存储相应行数据的聚集索引键，即主键。当通过辅助索引来查询数据时，InnoDB存储引擎会遍历辅助索引找到主键，然后再通过主键在聚集索引中找到完整的行记录数据。

MyISAM存储引擎索引实现

MyISAM索引文件和数据文件是分离的(非聚集)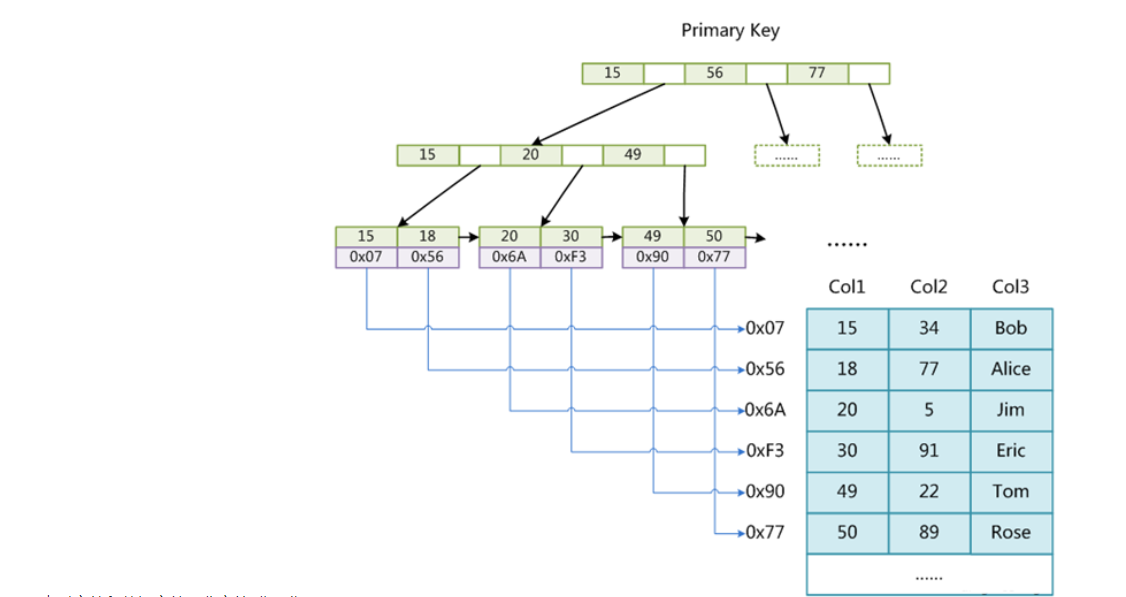
image

InnoDB存储引擎索引实现

InnoDB索引实现(聚集)

  • 表数据文件本身就是按B+Tree组织的一个索引结构文件
  • 聚集索引-叶节点包含了完整的数据记录

为什么建议InnoDB表必须建主键，并且推荐使用整型的自增主键？

如果表中没有定义主键，InnoDB 会选择一个唯一的非空索引（确切说会选择一个唯一非空的列作为主键）代替。如果没有这样的索引，InnoDB 会隐式定义一个主键来作为聚簇索引

聚簇索引的数据的物理存放顺序与索引顺序是一致的，即：只要索引是相邻的，那么对应的数据一定也是相邻地存放在磁盘上的。

聚簇索引的顺序和磁盘中数据的存储顺序是一致的，如果主键不是自增id，那么可以想 象，它会干些什么，不断地调整数据的物理地址、分页，当然也有其他一些措施来减少这些操作，但却无法彻底避免。但，如果是自增的，那就简单了，它只需要一页一页地写，索引结构相对紧凑，磁盘碎片少，效率也高。

为什么非主键索引结构叶子节点存储的是主键值？

(一致性和节省存储空间)

聚簇索引(主键索引)图

image

二级索引图

image

联合索引

联合索引结构

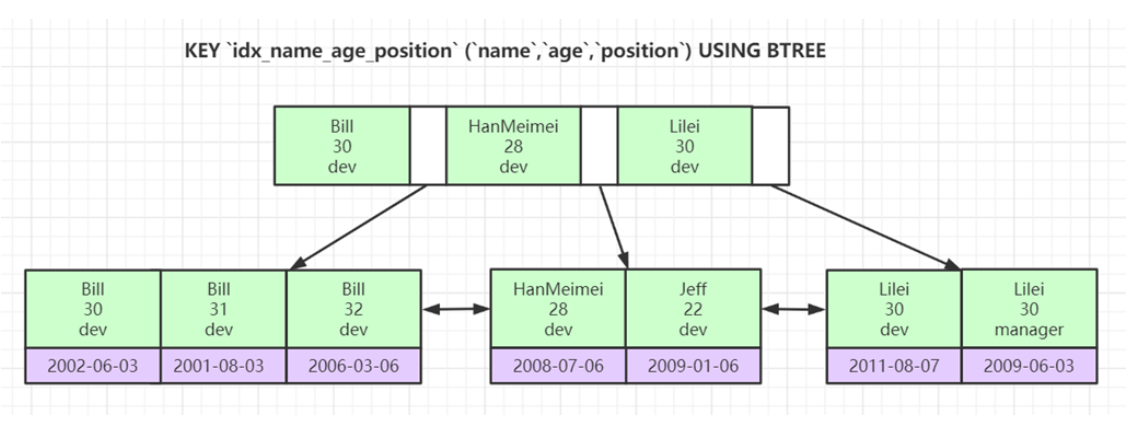
image

联合索引最左前缀原理

从联合索引的结构可以看出, 在前面的索引数据有序的情况下, 其后面索引数据的有序

如sql select * from user where name = 'Bill' and age = 31 and position = 'dev',在name等于Bill的情况下,其age是有序的, 这样age的索引也可以使用, 在age等于31的情况下, position也是有序的, position的索引也可以使用.

如sql select * from user where name in ('Bill', 'HanMeimei') and age = 31 and position = 'dev',此时查询出的索引数据age不再是有序的, 故age和position都不能走索引

所以在使用联合索引查询时, 我们应该尽量的保证所有索引可用, 把范围查询放在最后, 以充分的利用联合索引。

为什么要使用联合索引

减少开销

建一个联合索引(col1,col2,col3)，实际相当于建了(col1),(col1,col2),(col1,col2,col3)三个索引。每多一个索引，都会增加写操作的开销和磁盘空间的开销。对于大量数据的表，使用联合索引会大大的减少开销！

覆盖索引

对联合索引(col1,col2,col3)，如果有如下的sql: select col1,col2,col3 from test where col1=1 and col2=2。那么MySQL可以直接通过遍历索引取得数据，而无需回表，这减少了很多的随机io操作。减少io操作，特别的随机io其实是dba主要的优化策略。所以，在真正的实际应用中，覆盖索引是主要的提升性能的优化手段之一。

效率高

索引列越多，通过索引筛选出的数据越少。有1000W条数据的表，有如下sql:select from table where col1=1 and col2=2 and col3=3,假设假设每个条件可以筛选出10%的数据，如果只有单值索引，那么通过该索引能筛选出1000W10%=100w条数据，然后再回表从100w条数据中找到符合col2=2 and col3= 3的数据，然后再排序，再分页；如果是联合索引，通过索引筛选出1000w10% 10% *10%=1w，效率提升可想而知！

Innode存储引擎中, 通常一棵B+树可以存放多少行数据?

在计算机中磁盘存储数据最小单元是扇区，一个扇区的大小是512字节，而文件系统（例如XFS/EXT4）他的最小单元是块，一个块的大小是4k，而对于我们的InnoDB存储引擎也有自己的最小储存单元——页（Page），一个页的大小默认是16K(当然也可以通过参数设置)。

现在我们清楚了InnoDB中主键索引B+树是如何组织数据、查询数据的，我们总结一下：

  1. InnoDB存储引擎的最小存储单元是页，页可以用于存放数据也可以用于存放键值+指针，在B+树中叶子节点存放数据，非叶子节点存放键值+指针。

  2. 索引组织表通过非叶子节点的二分查找法以及指针确定数据在哪个页中，进而在去数据页中查找到需要的数据；

那么回到我们开始的问题，通常一棵B+树可以存放多少行数据？

这里我们先假设B+树高为2，即存在一个根节点和若干个叶子节点，那么这棵B+树的存放总记录数为：根节点指针数*单个叶子节点记录行数。

上文我们已经说明单个叶子节点（页）中的记录数=16K/1K=16。（这里假设一行记录的数据大小为1k，实际上现在很多互联网业务数据记录大小通常就是1K左右）。

那么现在我们需要计算出非叶子节点能存放多少指针，其实这也很好算，我们假设主键ID为bigint类型，长度为8字节，而指针大小在InnoDB源码中设置为6字节，这样一共14字节，我们一个页中能存放多少这样的单元，其实就代表有多少指针，即16384/14=1170。那么可以算出一棵高度为2的B+树，能存放1170*16=18720条这样的数据记录。

根据同样的原理我们可以算出一个高度为3的B+树可以存放：1170*1170*16=21902400条这样的记录。所以在InnoDB中B+树高度一般为1-3层，它就能满足千万级的数据存储。在查找数据时 一次页的查找代表一次IO， 所以通过主键索引查询通常 只需要1-3次IO操作 即可查找到数据。